Overview

The goal of this project is to develop Learning to Optimize, Control, and Adapt frameworks for control systems. The frameworks lie at the heart of Learning to Optimize (L2O) that is a class of scientific machine learning techniques that solves parametric optimization problems by learning how the optimization process depends on problem parameters. Rather than relying solely on generic, hand-designed solvers, L2O exploits problem structure and offline data to learn a mapping from parameters to near-optimal solutions or to accelerate iterative solver components. This project focuses on different key areas where L2O addresses fundamental challenges in Model Predictive Control (MPC) and Model Predictive Path Integral (MPPI) control:

Accelerating Real-Time Solvers: Solving complex constrained optimization problems, such as nonlinear or mixed-integer programs, at every time step is often intractable for systems with fast dynamics. We will demonstrate how L2O treats the MPC problem as parametric optimization, using learned models to predict optimal solutions given different problem parameters. We also cover how to embed constraints and objectives directly into the network architecture (e.g., via differentiable optimization layers or specialized loss functions) to improve constraint satisfaction and optimality.
Efficient Sampling for MPPI: Sampling-based methods like Model Predictive Path Integral (MPPI) control are powerful but computationally expensive due to the massive number of rollouts required. We will show how L2O can learn optimal sampling distributions, achieving high-performance control with significantly fewer rollouts and reduced computational cost.
Learning-to-Adapt (L2A): Beyond standard solving, we introduce L2A frameworks for dynamic environments. By formulating controller adaptation as a parametric optimization problem, where contextual variables act as parameters, L2O can learn strategies to adjust control parameters in real-time, enabling robustness to changing tasks and unobserved environmental conditions.

L2O for Mixed-Integer MPC

Summary

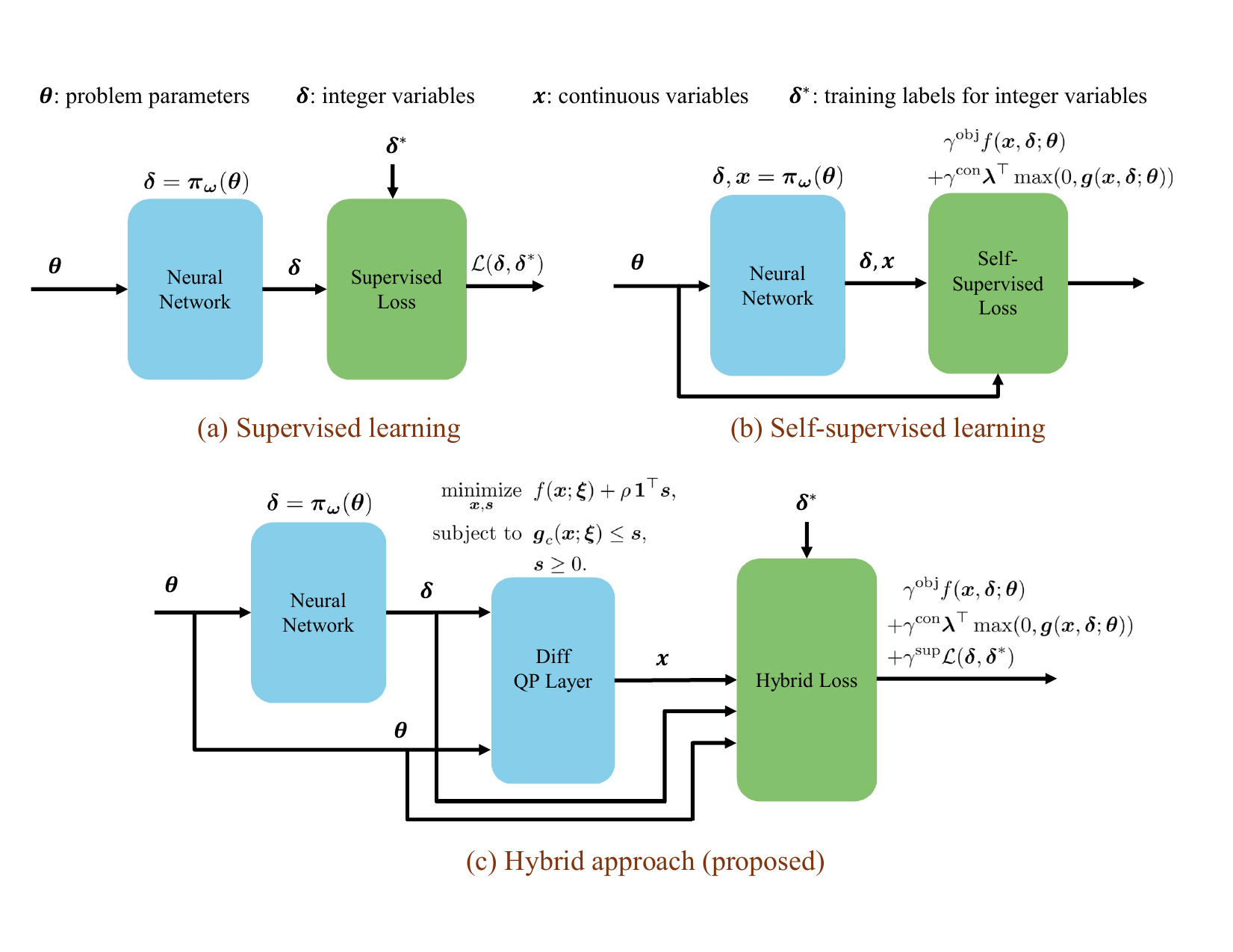
We propose a learning-to-optimize (L2O) framework for accelerating the solution of parametric MIQP problems by learning structured solution components directly from data. The key idea is to predict high-quality integer decisions using a neural network, while preserving exact continuous optimality by solving a differentiable quadratic programming (QP) layer conditioned on the predicted integers. By explicitly separating discrete and continuous variables, the framework leverages problem structure and improves both feasibility and performance. To train the model, we introduce a hybrid loss function that combines: (1) a supervised loss, encouraging predicted integer solutions to match globally optimal ones when labels are available, and (2) a self-supervised loss, derived directly from the MIQP objective and constraints, promoting feasibility and consistency even without labeled solutions.

Hybrid learning-to-optimize framework

Results

We evaluate the proposed hybrid L2O framework on two representative MI-MPC benchmarks: (1) Robot navigation with collision avoidance, where binary variables encode logical collision-avoidance constraints and interact strongly with continuous states and inputs, and (2) Thermal energy tank control, where integer variables directly appear in the objective function and govern operational modes.

Overall, the results demonstrate that the proposed hybrid learning-to-optimize (L2O) framework achieves a strong balance between feasibility and optimality across both benchmarks. These results highlight that combining supervised and self-supervised objectives is crucial for producing solutions that are both feasible and near-optimal in mixed-integer control problems.

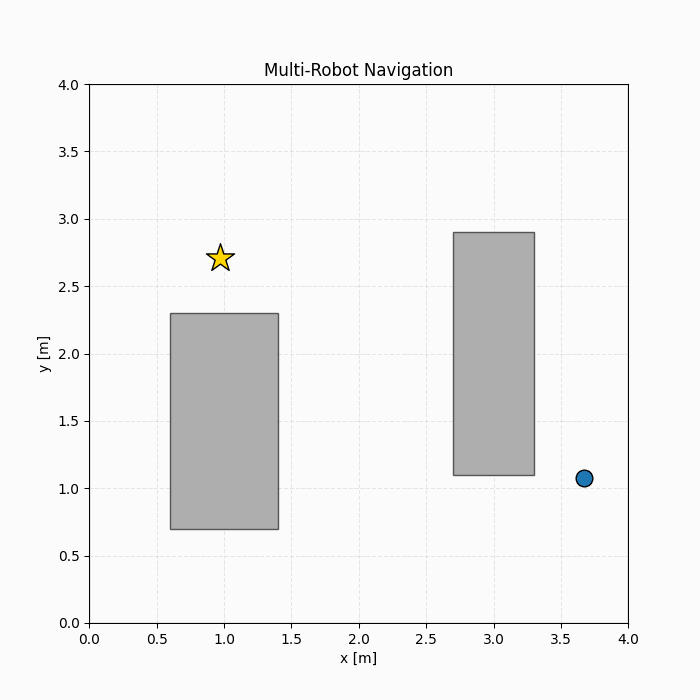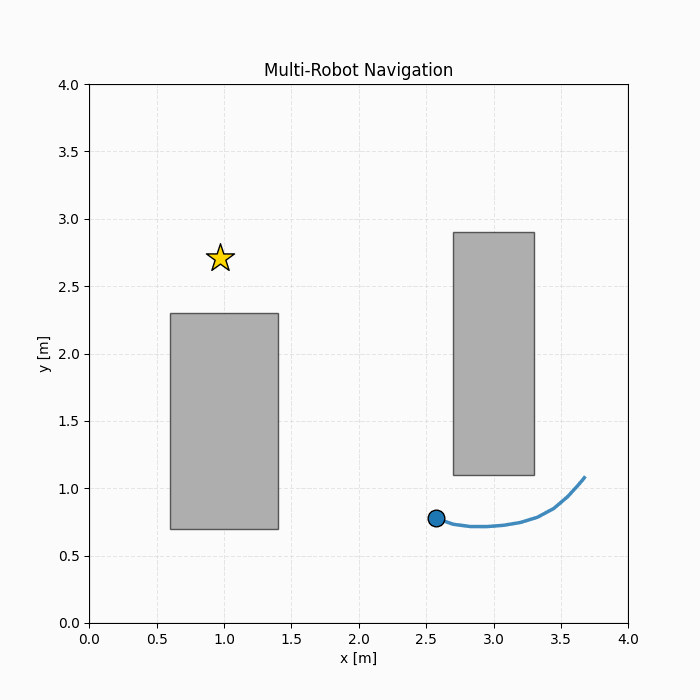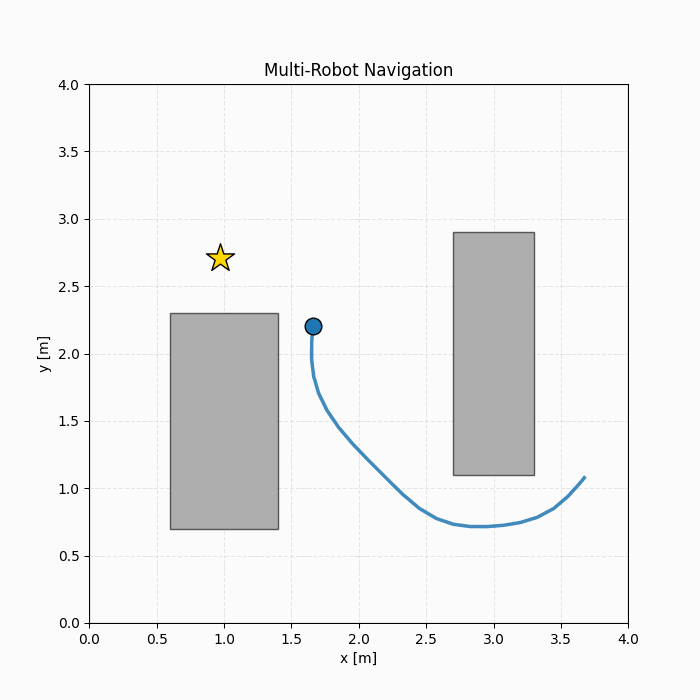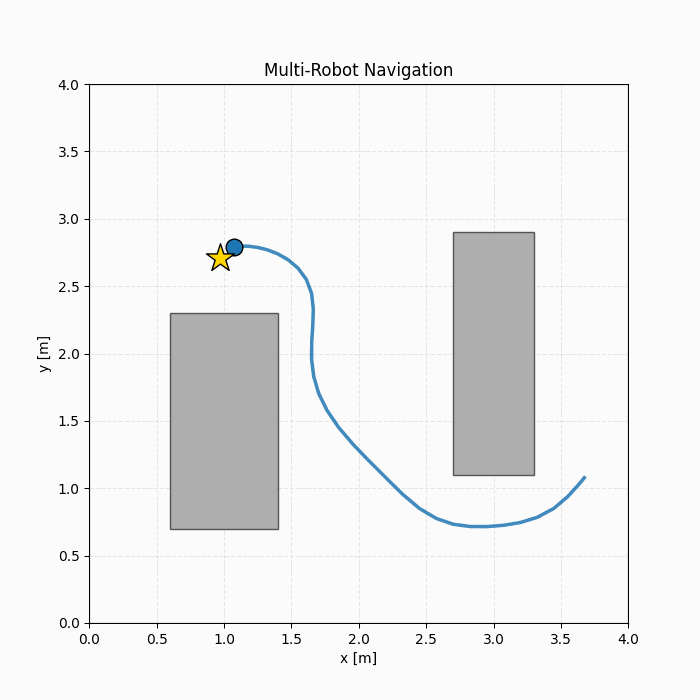
An example of robot navigation under mixed-integer MPC using L2O method.

Website

Code: GitHub Repository

Publications

A Hybrid Learning-to-Optimize Framework for Mixed-Integer Quadratic Programming
Viet-Anh Le, Mu Xie, Rahul Mangharam
8th Annual Learning for Dynamics \& Control Conference (L4DC), 2026
arXiv preprint

Contributors

Viet-Anh Le, Mu Xie, Rahul Mangharam

Citation


@inproceedings{le2026hybrid,
  title={A Hybrid Learning-to-Optimize Framework for Mixed-Integer Quadratic Programming}, 
  author={Le, Viet-Anh and Xie, Mu and Mangharam, Rahul},
  year={2026},
  booktitle={8th Annual Learning for Dynamics \& Control Conference},
}

L2O for Model Predictive Path Integral (MPPI) Control

Work in progress

Learning to Adapt

Work in progress