Overview
Atrial arrhythmia is a prevalent heart disease that results in weak and irregular contractions of the atria. It affects millions of people worldwide. Cardiac ablation is among the most successful treatment options. During the procedure, catheters are inserted into the left atrium to map the atrium geometry and record endocardium electrograms that are then converted into electro anatomical maps to pinpoint the arrhythmia source locations.
However, identifying arrhythmia sources is challenging. The electrograms are asynchronous and can be susceptible to noise. The spatial distribution of sampling sites is non-uniform, which leads to inaccurate maps. Identifying arrhythmia source locations is not a trivial task. Therefore, an ablation procedure often lasts from 3 to 6 hours, and arrhythmia recurrence within 12 months after first ablation is about 45%.
To address these challenges, we are developing an integrated computational heart model to guide left atrium arrhythmia ablation. Our system takes in the left atrium geometry and electrograms, processes them to extract regional tissue properties, which are used to tune a heart model, creating a patient-specific whole-atrium model. With this model, we can simulate and detect arrhythmia sources, and provide ablation assistance. To build such a system, we investigated the fiber effects on atrial activation patterns. So far, we developed a fast heart model tuning method which takes only a few seconds of computation time on a personal computer, enabling real-time assistance during the ablation procedure. Current results show we achieve high accuracy in simulating arrhythmias, which we validated on patient data.
Computational Heart Model
The overview process of patient-specific heart modeling is: extract patient data to tune heart model parameters, next, initiate arrhythmia (the heart’s initial state is also extracted from patient data), then solve the heart model equations to simulate patient-specific arrhythmias.
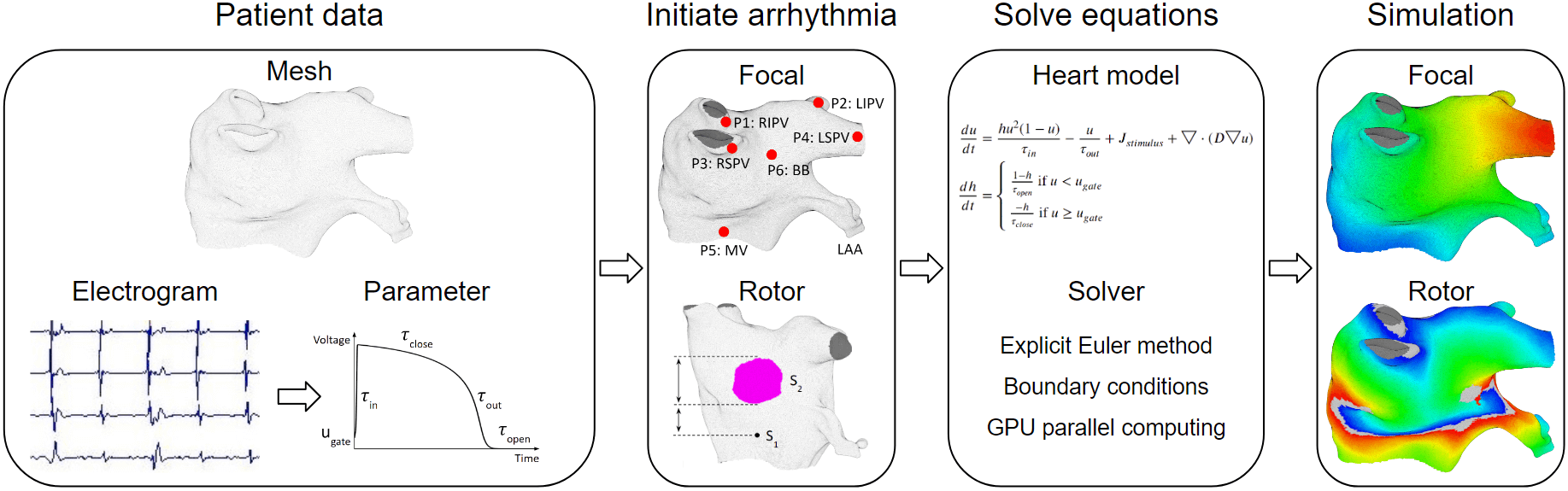
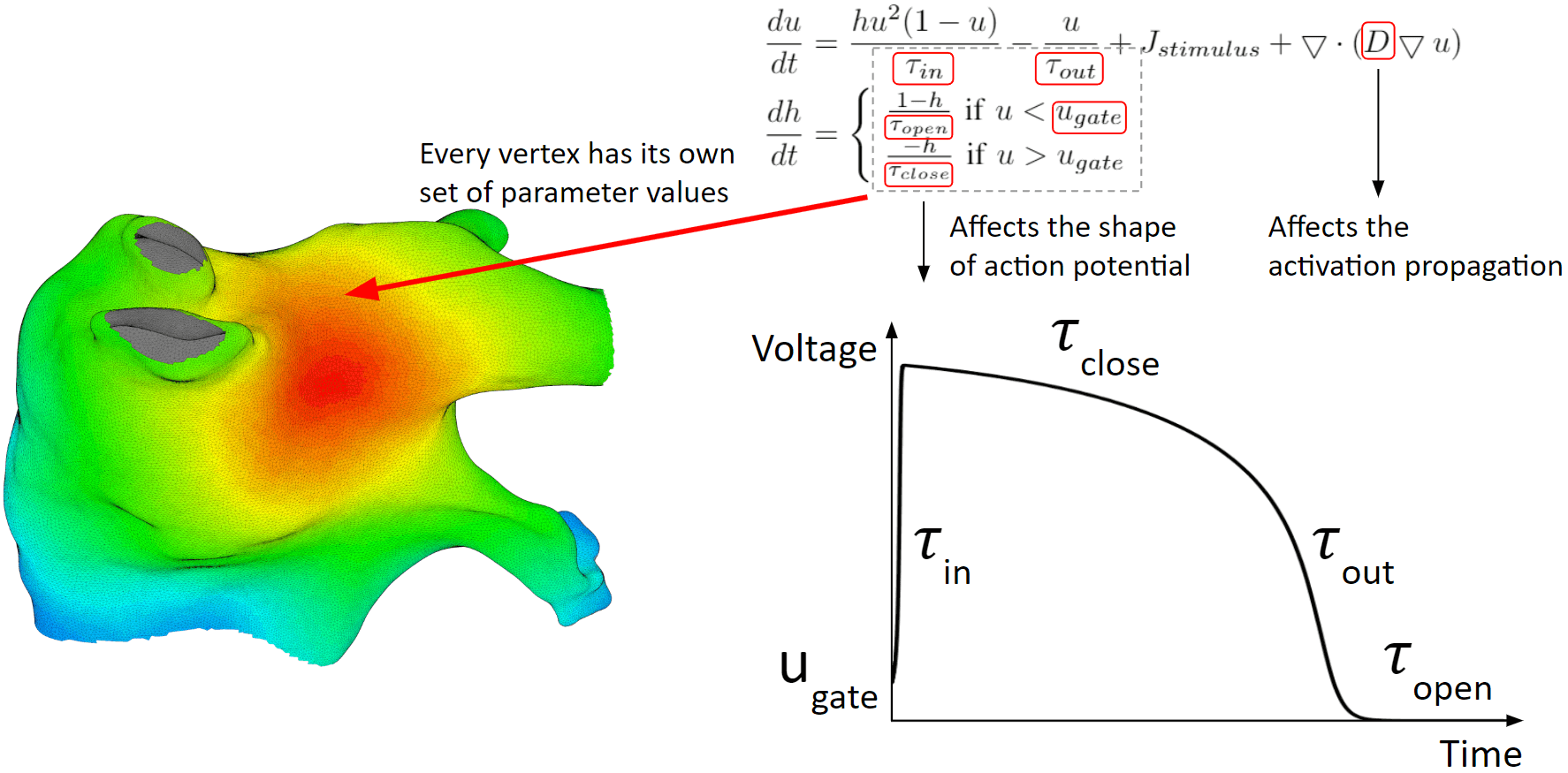
Below are the heart model equations. They calculate the activation action potentials. There are parameters that affect the shape of the action potential, and parameters that affect the activation propagation. These parameters are tuned locally. Every vertex of the mesh has its own set of parameter values.
Spatial Discretization
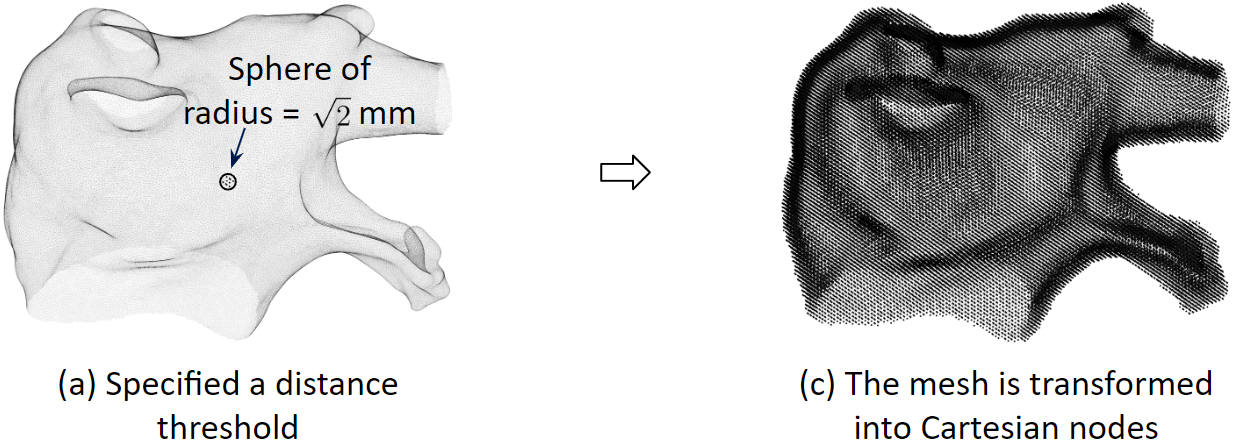
To solve the heart model equations, we discretize the left atrium in space. We transform the 3D triangular mesh into Cartesian nodes. For a mesh vertex, Cartesian nodes within a radius are created. And for every vertex, we create the associated cartesian nodes. As a result, the Cartesian nodes will wrap around the mesh.
Temporal Discretization
We discretize the heart model equations in time using the explicit Euler method. With some initial values at time 0, we can compute the values of the next time step.
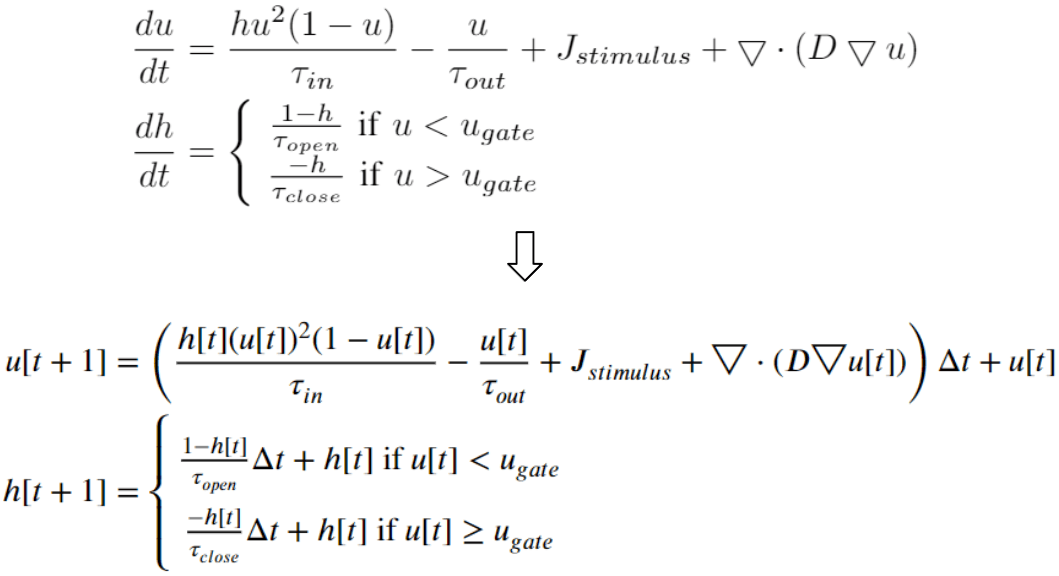
Diffusion Modeling
To compute the diffusion term, we assumed no-flux boundary conditions, and used a 19-node stencil. The action potential of the red node will be diffused into its 18 neighbors according to the diffusion coefficient matrices.

Arrhythmia Simulation Examples
Here are examples of arrhythmia simulations.
- Focal arrhythmia: Activation originates at an abnormal location.
- Rotor arrhythmia: Spiral waves cause irregular heartbeat.
- Zigzag propagation: Complex scar distributions create activation tunnels of various conduction velocities.
- Atrial fibrillation: Chaotic activation waves that have no organizations.
Diffusion Coefficient Tuning
Our solution to the lack of fiber data is to compensate that with a diffusion coefficient tuning. Tuning is challenging:
- Heart model is nonlinear.
- Diffusion is influencing the neighbor nodes, not the immediate vicinities.
- Sensitive to the initial guess values, adjustment steps, ending criteria, etc.
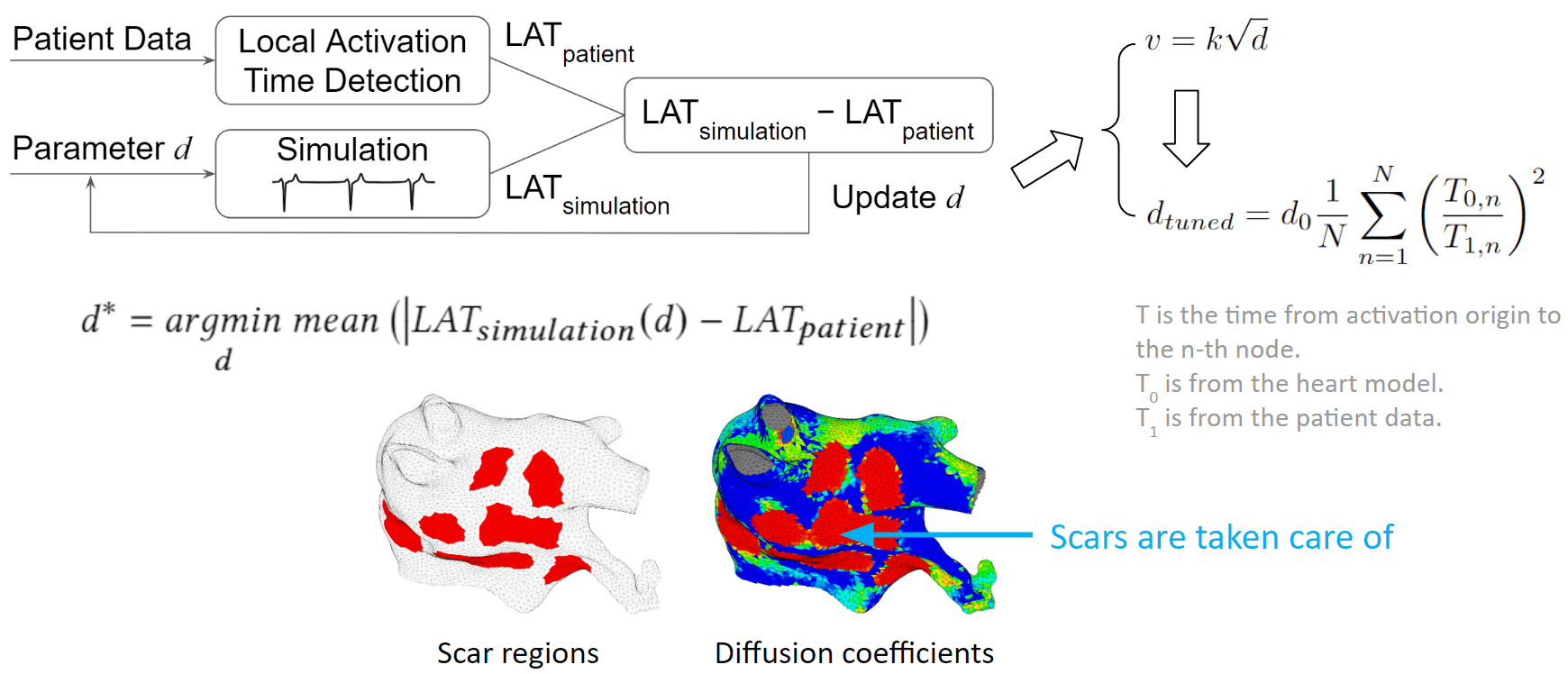
We developed an optimization process to overcome the tuning challenges. We process the patient data to obtain the true local activation times. Then we run a simulation with some initial guess diffusions, and process the simulation result to obtain the simulated local activation times. These two sets of activation times are compared and the diffusion values are updated according to this comparison. New simulations are run and diffusion values are adjusted in each iteration. The tuning is done when the difference between patient activation time and simulation activation time is minimized.
To make the tuning faster, we exploit the relation between conduction velocity and diffusion coefficient, which reduces the number of iterations needed to reach the optimum.
As illustrated in the figure below, we can see that scars are taken care of too. The figure on the left shows scar regions in red, and the figure on the right, shows a diffusion coefficient map, where red represents low conductivity. The red regions between these two figures are almost the same. Which means the tuning is accurate.
Experimental Results
Our model achieved high accuracy of simulating arrhythmias. We ran experiments on 7 patient’s left atrium.
Focal Arrhythmia
For focal arrhythmia, we achieved activation time accuracy of 96%.
Rotor Arrhythmia
For rotor arrhythmia, we achieved activation time accuracy of 93%.
Patient Validation Studies
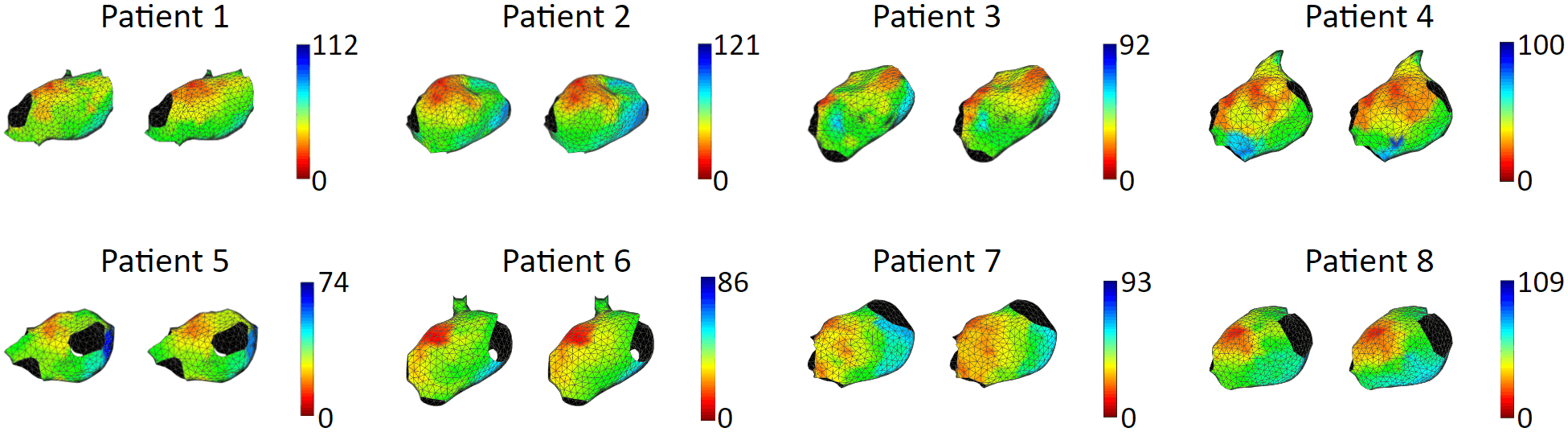
We tested our model with 15 patient data, to show that our model is capable of accurately reproducing patient arrhythmias.
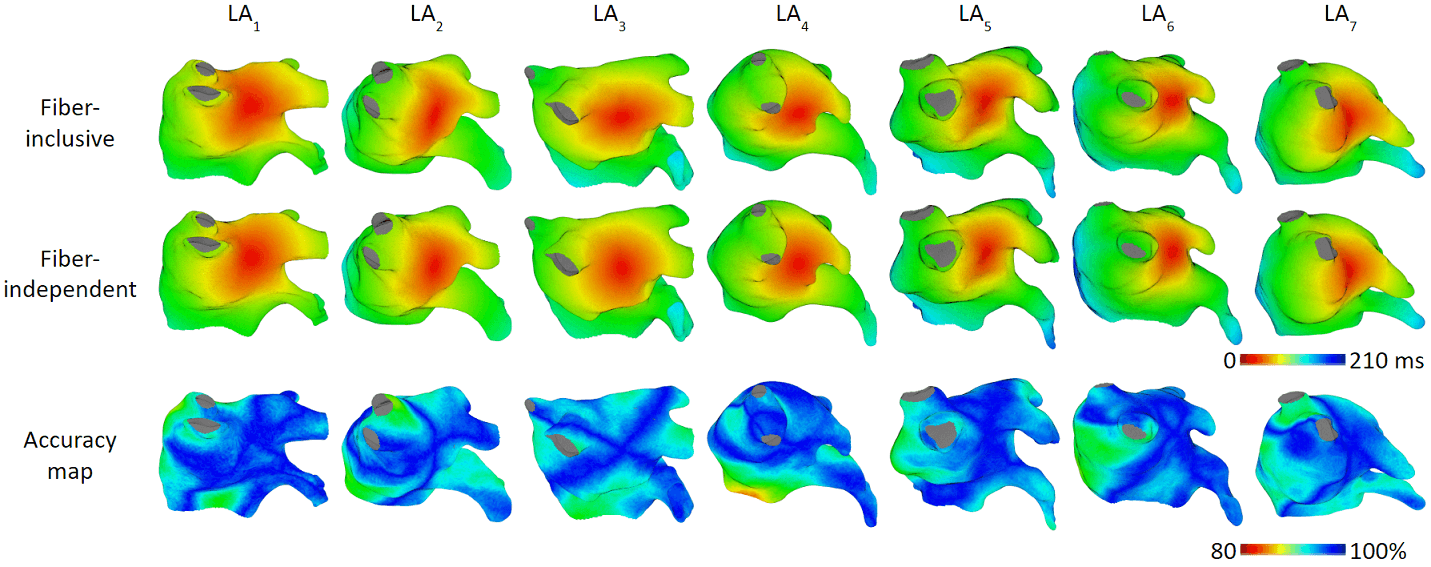
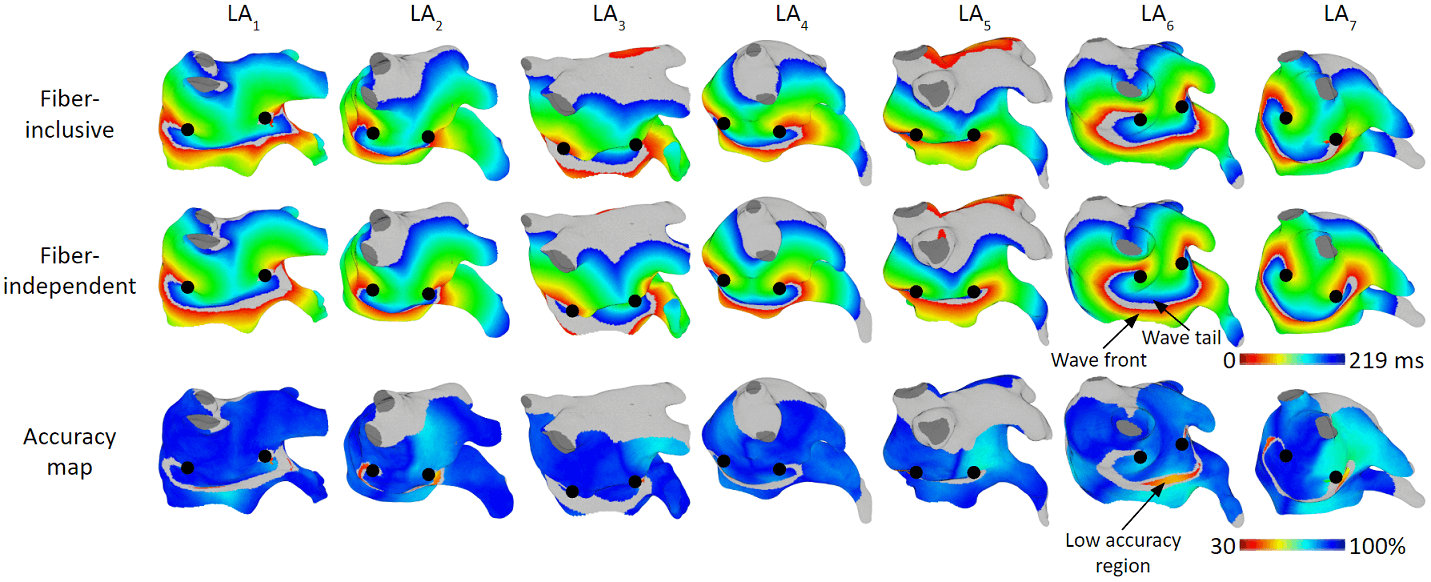
The figures below are the results of 7 atrial tachycardia maps. We achieved an average activation time error of 10.97 ms, with an average correlation of 0.81.
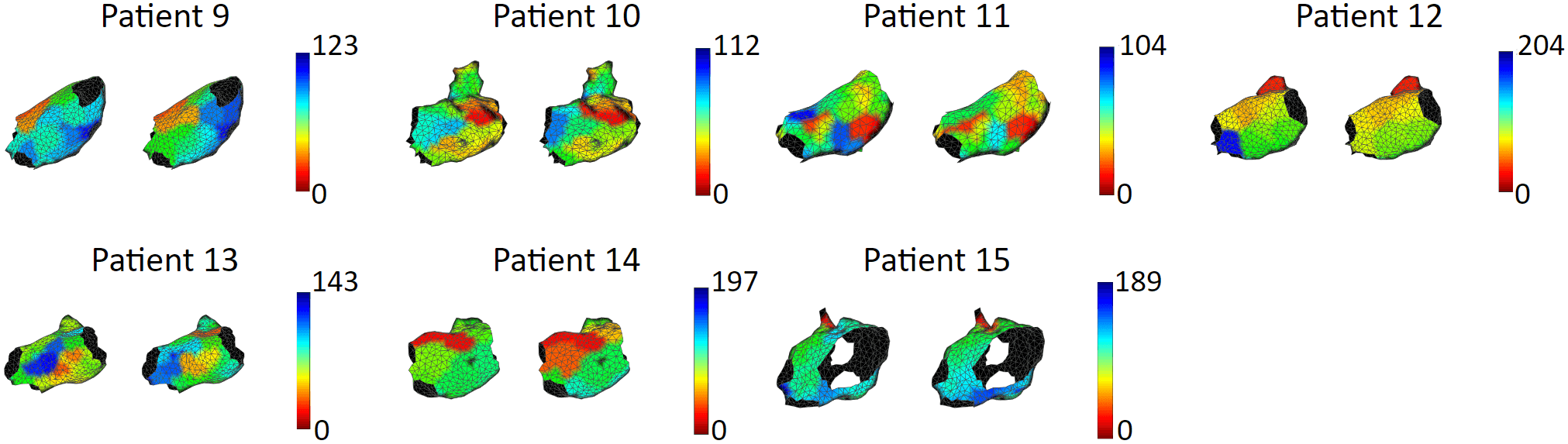
These are the results of 8 sinus rhythm maps. We achieved an average activation time error of 5.47 ms, with an average correlation of 0.95. Sinus rhythm maps are helpful: Oftentimes, patient comes in the operating room in sinus rhythm, or will get cardioversion into sinus rhythm, to acquire a voltage map for assisting pulmonary vein isolation.
Publications
-
Individualization of atrial tachycardia models for clinical applications: Performance of fiber-independent model
Jiyue He, Arkady Pertsov, John Bullinga, Rahul Mangharam
IEEE Transactions on Biomedical Engineering, 2023. -
Fiber Organization Has Little Effect on Electrical Activation Patterns during Focal Arrhythmias in the Left Atrium
Jiyue He, Arkady M. Pertsov, Elizabeth M. Cherry, Flavio H. Fenton, Caroline H. Roney, Steven A. Niederer, Zirui Zang, Rahul Mangharam
IEEE Transactions on Biomedical Engineering, 2023.
Feature Article -
Tachycardia Activation Pattern Predictivity of a Fiber-Independent Left Atrium Model
Jiyue He, Arkady Pertsov, John Bullinga, Rahul Mangharam
Cardiac Physiome Society, 2023. -
Real-Time Atrial Tachycardia Ablation Guidance with a Left Atrium Model
Jiyue He, Arkady Pertsov, Rahul Mangharam
Heart Rhythm Society, 2023. -
Patient-Specific Heart Model towards Atrial Fibrillation
Jiyue He, Arkady Pertsov, Sanjay Dixit, Katie Walsh, Eric Toolan, Rahul Mangharam
Proceedings of the ACM/IEEE 12th International Conference on Cyber-Physical Systems (ICCPS), May 2021. -
Electroanatomic Mapping to Determine Scar Regions in Patients with Atrial Fibrillation
Jiyue He, Kuk Jin Jang, Katie Walsh, Jackson Liang, Sanjay Dixit, Rahul Mangharam
41st International Engineering in Medicine and Biology Conference (IEEE EMBC), July 2019.
Contributors
Jiyue He, Arkady Pertsov, Sanjay Dixit, Katie Walsh, Eric Toolan, Rahul Mangharam
Citation
@inproceedings{10.1145/3450267.3450532,
author = {He, Jiyue and Pertsov, Arkady and Dixit, Sanjay and Walsh, Katie and Toolan, Eric and Mangharam, Rahul},
title = {Patient-specific heart model towards atrial fibrillation},
year = {2021},
isbn = {9781450383530},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/3450267.3450532},
doi = {10.1145/3450267.3450532},
booktitle = {Proceedings of the ACM/IEEE 12th International Conference on Cyber-Physical Systems},
pages = {33–43},
numpages = {11},
location = {Nashville, Tennessee},
series = {ICCPS '21}
}